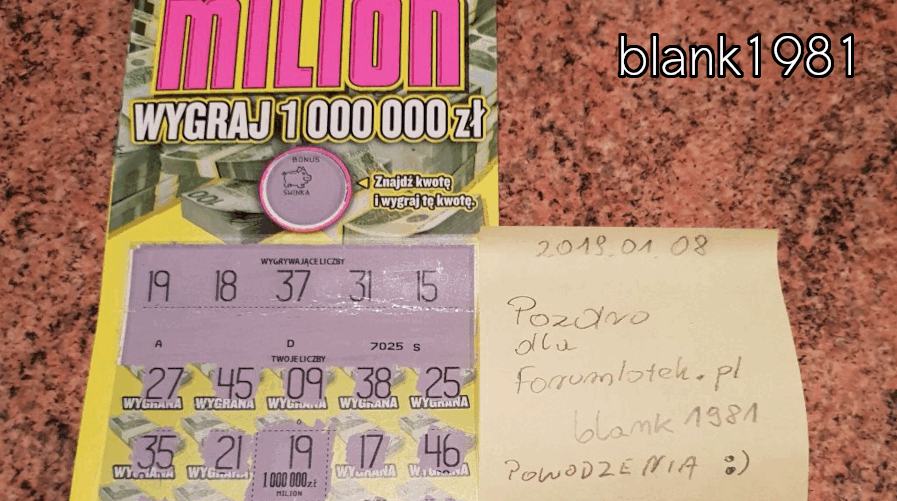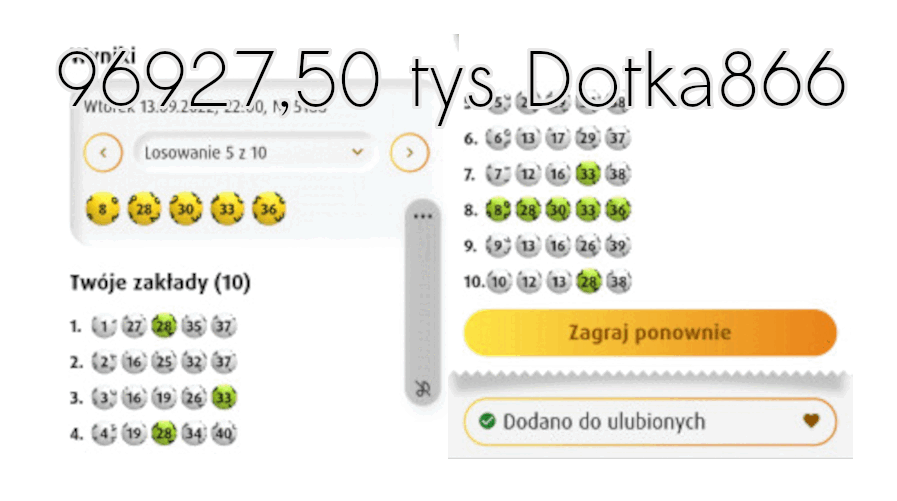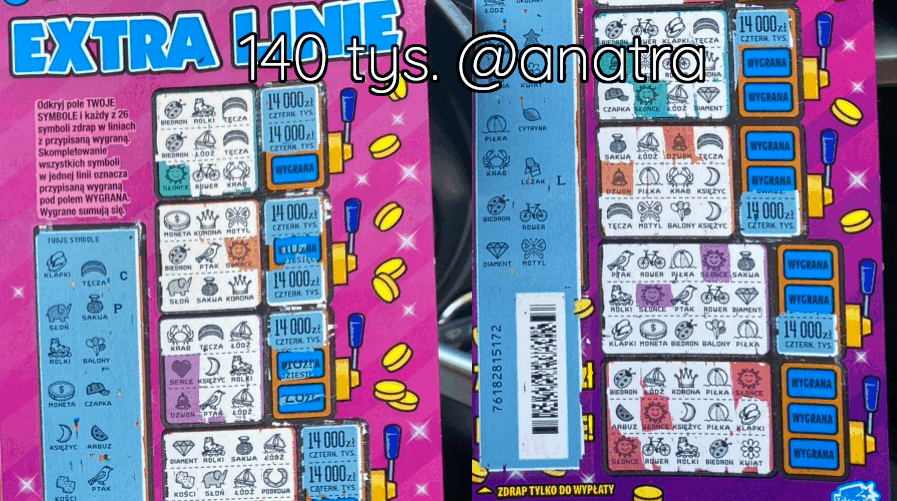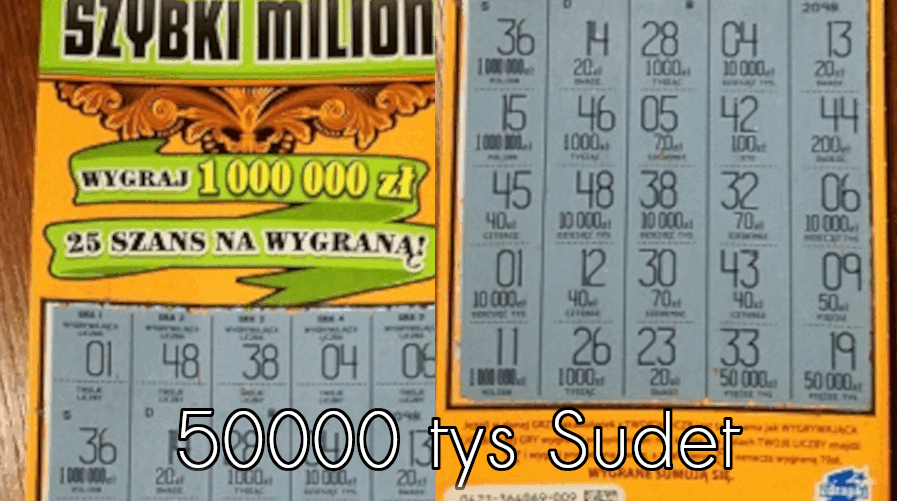
Typowanie liczb LOTTO
-
Belzebabka
- Cwaniak
- Posty: 379
- Rejestracja: 14 wrz 2023, 18:02
- Kontakt:
Re: Typowanie liczb LOTTO
Przejrzałeś już 15 postow, aby zobaczyć więcej . Zaloguj
- Michalrsko
- Mistrz 4/5
- Posty: 2909
- Rejestracja: 04 sty 2022, 0:21
- Kontakt:
Re: Typowanie liczb LOTTO
Mogę płacić więcej -ale nie dychę  żeby były większe wygrane za 3ki i 4ki
żeby były większe wygrane za 3ki i 4ki
A big dream to travel far...
-
System
- Maniak
- Posty: 792
- Rejestracja: 19 kwie 2024, 9:41
- Kontakt:
Re: Typowanie liczb LOTTO
To , że płacą śmieszna kwotę za trójkę to wiemy.
A u mnie postępy bo ostatnio wpadły dwie dwójki na trzy zakłady
A u mnie postępy bo ostatnio wpadły dwie dwójki na trzy zakłady

- Michalrsko
- Mistrz 4/5
- Posty: 2909
- Rejestracja: 04 sty 2022, 0:21
- Kontakt:
Re: Typowanie liczb LOTTO
Krok po kroku jeszcze trochę i trójczyna wpadnie 
A big dream to travel far...
-
Goldfinger
Re: Typowanie liczb LOTTO
Po bardzo długiej nieobecności wygranej, trafiona 3ka 24zl
- Załączniki
-
- IMG_3594.jpeg (622.42 KiB) Przejrzano 1479 razy
- pablovsky
- Uzależniony od gry
- Posty: 916
- Rejestracja: 13 lut 2024, 1:19
- Kontakt:
Re: Typowanie liczb LOTTO
Graj dalej, powinno zadziałać sławetne "prawo serii". Oby się potwierdziło, 3mam kciuki.
- Michalrsko
- Mistrz 4/5
- Posty: 2909
- Rejestracja: 04 sty 2022, 0:21
- Kontakt:
-
Goralka
- Cyc
- Posty: 5
- Rejestracja: 13 sty 2024, 23:15
- Kontakt:
Re: Typowanie liczb LOTTO
Według mnie oczywiście, że jest logika losowości. Prawdopodobieństwo jest tak kluczącą nauka, tak jeszcze nierozgryziona, że na Marilyn coś Savant rzucili się wszyscy ci, którzy ta naukę "tworzyli", profesorowie, matematycy, wszyscy, bo powiedziała coś, co się nie zgadzało z powszechnie przyjęta nauka o prawdopodobieństwie. A jak się okazało nie matematycy mieli rację, tylko Marilyn, która obaliła ich wiedzę i ta naukę o prawdopodobieństwie.
Prawdopodobieństwo rządzi się własnymi prawami i myślę, że nie do końca tymi, które są powtarzane w książkach, które zresztą sobie przeczą.
Prosty przykład, kiedy prawdopodobieństwo samo sobie przeczy. Wszyscy twierdzą, że prawdopodobieństwo wypadnięcia dziś 12345 jest takie samo jak każdej innej liczby. To oczywiście prawda. Ale jednocześnie mówią, że zdarzenia są od siebie zupełnie niezalezne i prawdopodobieństwo jest takie samo jak wypadnięcie każdego innego zestawu liczb. To wyobraź sobie sytuację, kiedy od początku kiedy istnieje totek wypadają codziennie liczby 12345 i żadne inne. Oczywiście nieprawdopodobne. Tu jest zgrzyt całej nauki prawdopodobieństwa, która sobie przeczy: dlatego, że zdarzenia niby są od siebie niezalezne i może wypadać codziennie co chce (nawet to samo od tysiąca losowań), a jednak nie mogą dać jednego punktu na wykresie tak, jakby inne liczby nie istniały, bo biorąc zestaw liczb np. z tysiąca losowań, liczby muszą się ułożyć w dzwon. Jeśli się nie ułożą, to oznacza, że doszło do oszustwa zwyczajnie. Muszą, tak mówi to samo prawdopodobienstwo. A skoro muszą się ułożyć w dzwon, to nie może wypadać tylko jeden zestaw liczb. A skoro nie może wypadać tylko jeden zestaw liczb, to jednak liczby są od siebie w jakiś sposób zależne i prawdopodobieństwo wypadnięcia 12345 każdego dnia wcale nie jest takie samo, bo inaczej nie istniałby warunek istnienia rozkładu np. dzwona.
Sprzeczność nauki o orawdopodobienstwie jest i myślę, że kwestia (długiego, pewnie nie wiadomo czy za naszego życia) czasu jest, kiedy podważone zostanie elementy tego, czego do tej pory uczą.
-
aera
- Cwaniak
- Posty: 238
- Rejestracja: 21 lis 2023, 20:40
- Kontakt:
1 Inni to lubia
Re: Typowanie liczb LOTTO
Do tej pory odbyło się ponad 7 tys. losowań lotto. Prawdopodobieństwo wypadnięcia 123456 to prawie 1:14 milionów. Obawiam się, że ta kombinacja może nigdy nie paść, ani żadna z naszych ulubionych, magicznych, czy jakiś tam bardziej czy mniej urojonych kombinacji
- ER33
- Moderator
- Posty: 7389
- Rejestracja: 16 lip 2018, 11:49
- Lokalizacja: Gdańsk
- Kontakt:
1 Inni to lubia
Re: Typowanie liczb LOTTO
Odkopać mój wpis z września 2020 roku
To dopiero jest prawdopodobieństwo zdarzenia i logika losowości
Kto jest online
Użytkownicy przeglądający to forum: Obecnie na forum nie ma żadnego zarejestrowanego użytkownika i 9 gości